数学検定準1級を勉強しています、カテナリーです。
今回は数列の和の記号シグマとその和の公式について。
しばらく勉強していないとこの式もうろ覚えになりがちですね。
この記事では、
3パターンあるシグマの公式を覚え方と共に紹介していきます。
シグマの公式は、とりあえずkだけ丸暗記で。
あとはそのkが\(k^2\)と\(k^3\)とどう違うのかを覚えます。
シグマの公式一覧
シグマの公式は以下の3式です。
kの時は、等差数列の初項1、公差1なので等差数列の和の
公式に \( a=1,d=1 \) を代入すれば成立します。
\( k^2 , k^3 \)の時は、・・・を使えば証明できますが、
少しやっかいなので、今回は省略します。
気になる方はこちらが参考になると思います。↓

$$ \displaystyle \sum_{k=1}^{n}k = \frac{1}{2}n(n+1) $$
$$ \displaystyle \sum_{k=1}^{n}k^2 = \frac{1}{6}n(n+1)(2n+1) $$
$$ \displaystyle \sum_{k=1}^{n}k^3 = \{ \frac{1}{2}n(n+1) \} ^2 $$
kの式とk^2およびk^3との相違点
\( k^2 , k^3 \)の式を、kの時との相違点で色付けしてみます。
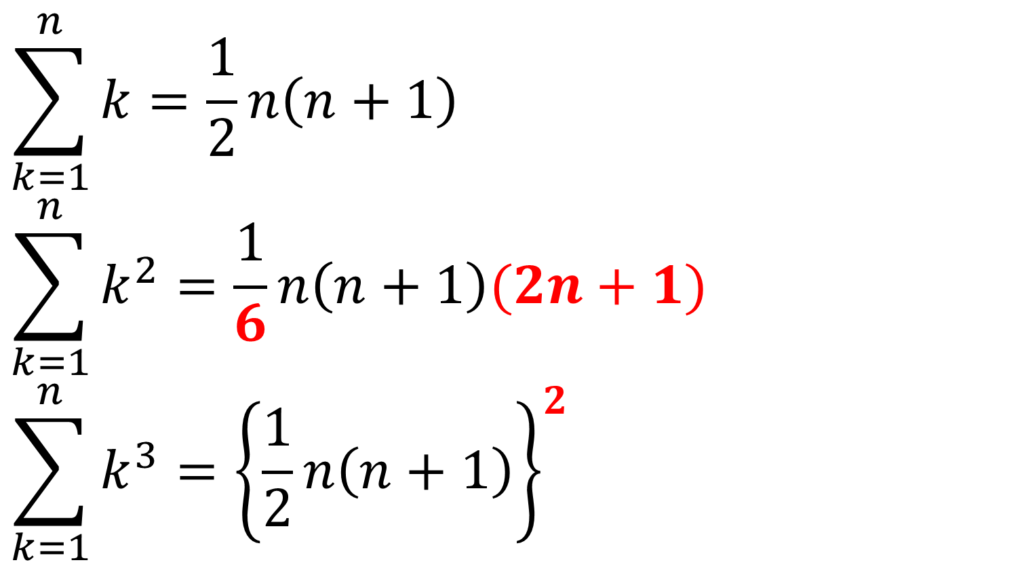
\( k^2 \)は、
- 分母が「6」
- (2n+1)が掛けられている
\( k^3 \)は、
- kの時の公式を2乗したもの
という3つの相違点があります。
この違いを覚えましょう。
まとめ
まとめると次のようにも表記できます。
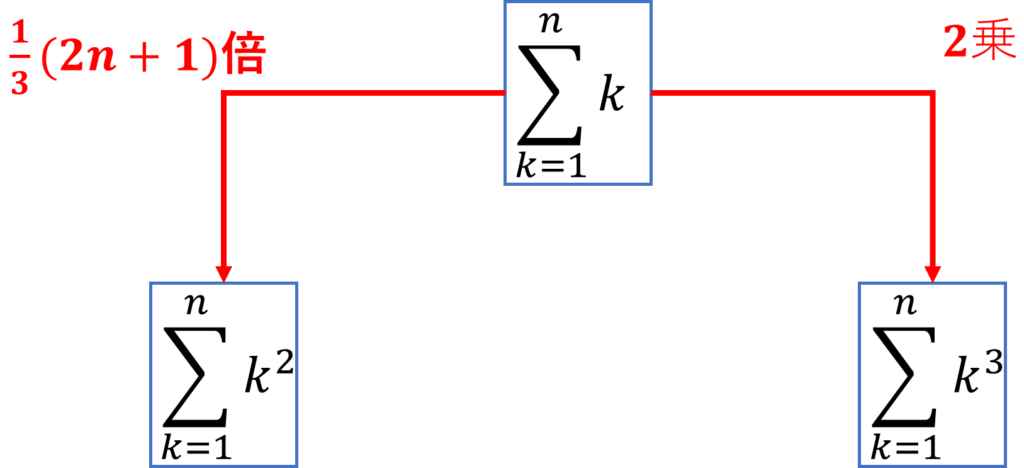
\( k^2 \)の式は、\( \frac{1}{3}(2n+1) \)倍するものと覚えるよりも、
分母が6に変わっていることと(2n+1)掛けていることを、
\( k^3 \)は、\( k \)を2乗するで覚えてOKです。
数学検定の勉強で復習していましたが、
これで少しは一式丸暗記を避けられそうな気がします。
手短でしたが、今回はここまで。



コメント