数学検定準1級の勉強進めています。カテナリーです。
問題集を1冊買って、現在「数列」の単元を勉強中です。
数列の和に関しては、かなりうろ覚えの状態だったので
今回は等差・等比数列の和の計算を復習し、その備忘録を記していきます。
この記事では、うろ覚えになっていた等差数列および等比数列の和を
公式とその求め方を3分くらいで理解できるものにまとめてみました。
等差数列
等差数列の和
等差数列の第1項から第\(n\)項は、次のように表せます。
$$ S_n = \frac{n}{2}(a_1 + a_n) $$
$$ S_n = \frac{n}{2}(2 a_1 + d (n-1)) $$
では求め方を次の章にて。
等差数列の和の公式の求め方
第1項と第\(n\)項の和、第2項と第\(n-1\)項の和・・・
がそれぞれ同じになることを利用します。
その時の和は、\( 2 a_1 + d (n-1)\) で、これは
\(n\)が偶数の時は\( \frac{n}{2}\)個
\(n\)が奇数の時は\( \frac{n-1}{2}\)個
出てきます。
\(n\)が奇数の時
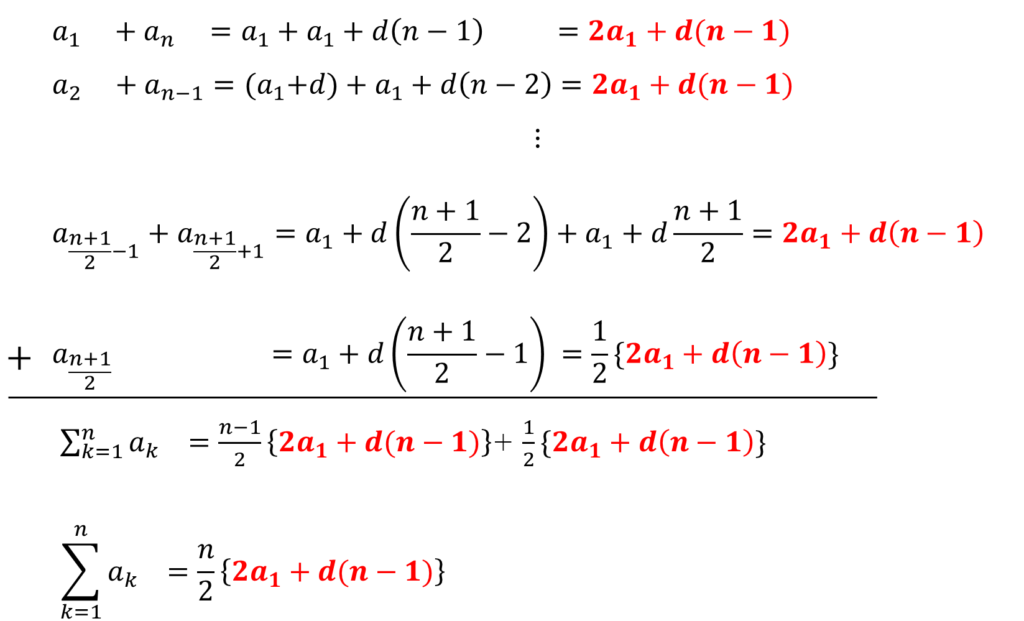
\( 2 a_1 + d (n-1)\) が\( \frac{n-1}{2}\)個と、
数列の真ん中になる\( \frac{n+1}{2} \)番目が、\( \frac{1}{2} \{ 2 a_1 + d (n-1) \} \)と
表されるので、\( 2 a_1 + d (n-1)\) が合計\( \frac{n}{2}\)個分出てきます。
よって、最初に示したような公式を導くことができます。
同様に\(n\)が偶数の時

\( 2 a_1 + d (n-1)\) が\( \frac{n}{2}\)個分出てくるので、
同じ式となり証明出来ました。
等比数列
等比数列の和
等比数列の和は次の通り。ただし \( r \not= 1 \)
$$ S_n = \frac{a_1 ( 1- r^n)}{(1-r)} = \frac{a_1 ( r^n – 1 )}{(r-1)} $$
\(r=1\)の時は、初項が\(n\)個分つづくだけなので、
和は次のようになります。
$$ S_n = na_1 $$
等比数列の和の公式の求め方
\( r \not= 1 \) の時の公式は、次のように説明できます。
等比数列の和である\( S_n \)と、それをr倍したものを
引き算する要領で証明します。
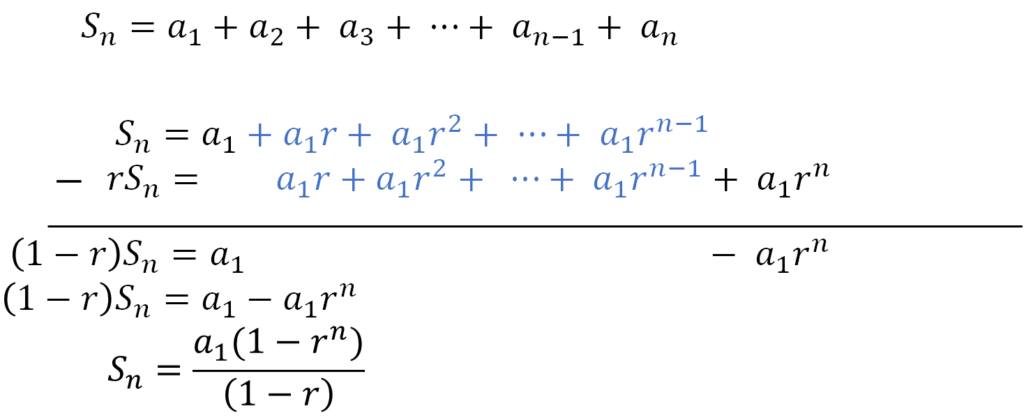
青字の部分が引き算により消えるので、
式が以上のように残るので、これをまとめると先に示した
等比数列の和となります。
今回はここまで。等差・等比数列の和の備忘録でした。
次回は同じくうろ覚えになっているシグマの公式計算を・・・。



コメント