準1級に向けて勉強中、どうもカテナリーです。
今回は三角形の内角の二等分線についてのまとめ記事です。
この内容は数学IAの範囲ですが、準1級の出題範囲にある
ベクトルでも使う羽目になるので・・・。
久々に目の前にして分からなくなってしまったので
今回記事にしたということです。
ポイントは以下の通り。
- △ABCにおいて∠Aの内角と外角の二等分線における
内分および外分の辺の比はどちらもAB:AC=BD:CDとなる。 - 内分および外分の比は三角形の比に平行な補助線を
引くことで証明可能 - ベクトルでの表記は座標で表す時と同様に符号に注意
内角の二等分線による内分
△ABCについて∠BACの二等分線を引き、
線分BCの交点を点Dとすると、図は次の通りになります。
ただし、説明用に線分ABの長さを4、線分ACの長さを6とします。
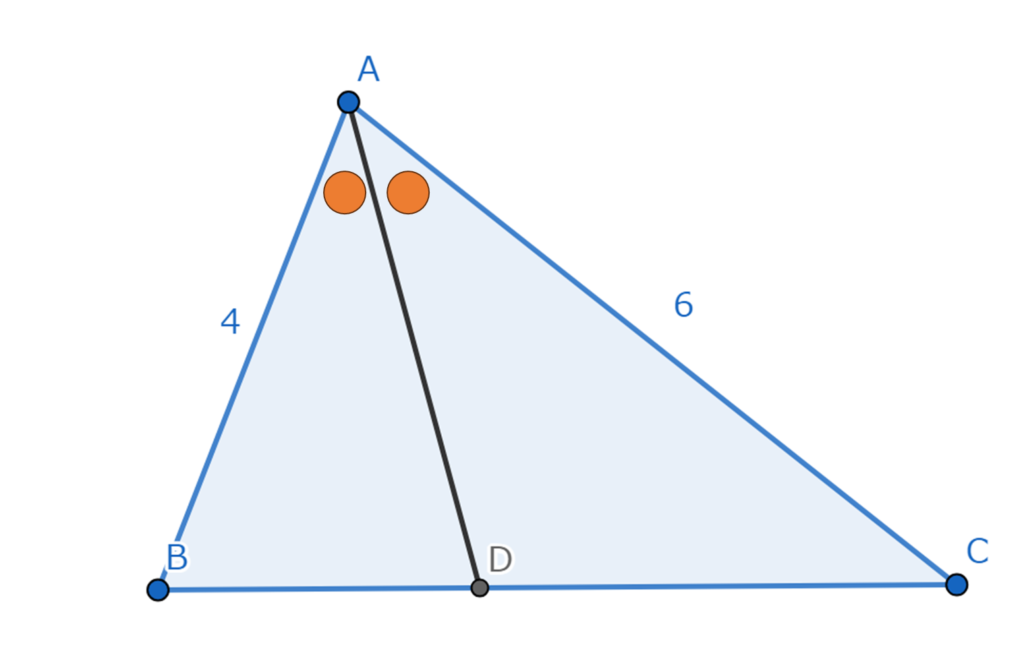
ここに補助線を引きます。
線分ADに平行で、点Cを通る直線と直線ABの交点をEとして線を引きます。
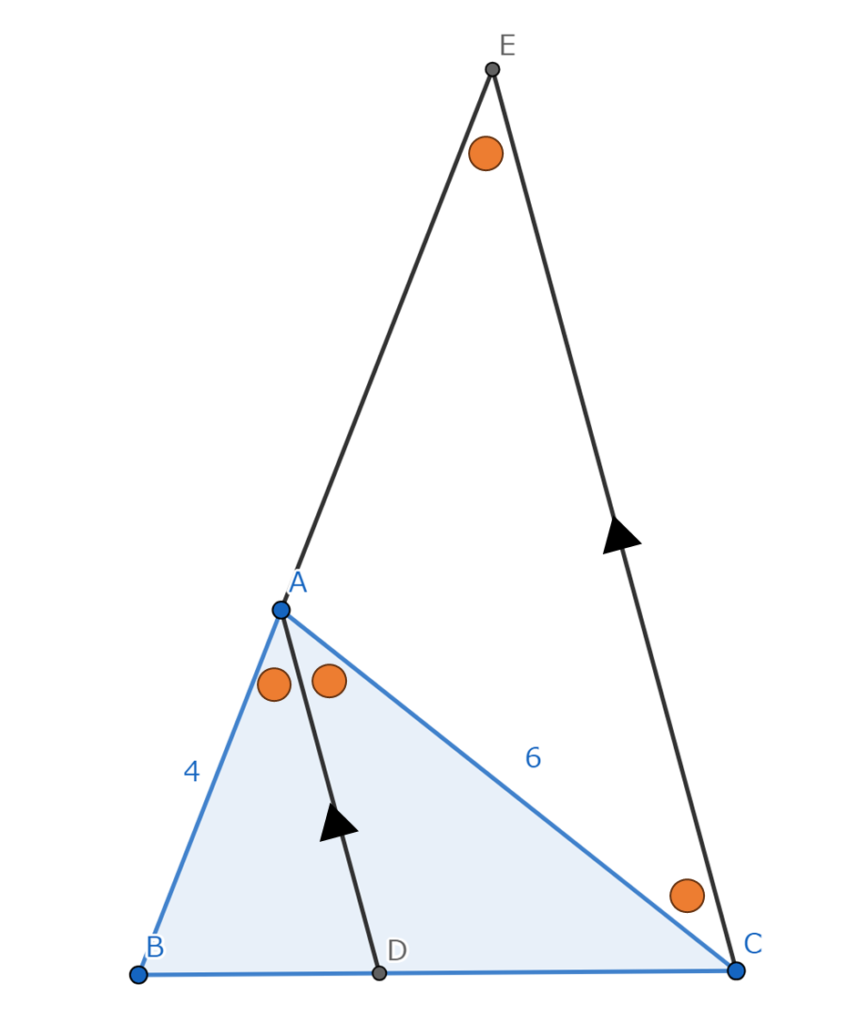
すると上の図のようになり以下のことが言えるようになります。
∠ACE=∠AECより△AECは二等辺三角形なのでAC=AE=6 …①
AD\(/\!/\)ECより、AB:AE=BD:DC …②
①②よりAB:AC=BD:DC=4:6=2:3
このことから内角の二等分線は、その内角の向かい合う辺を
隣り合う辺の長さの比で内分することになります。
以上の例から三角形の内角の二等分線とその内角に向かい合う線分との交点は
次のような一般式で内分できます。
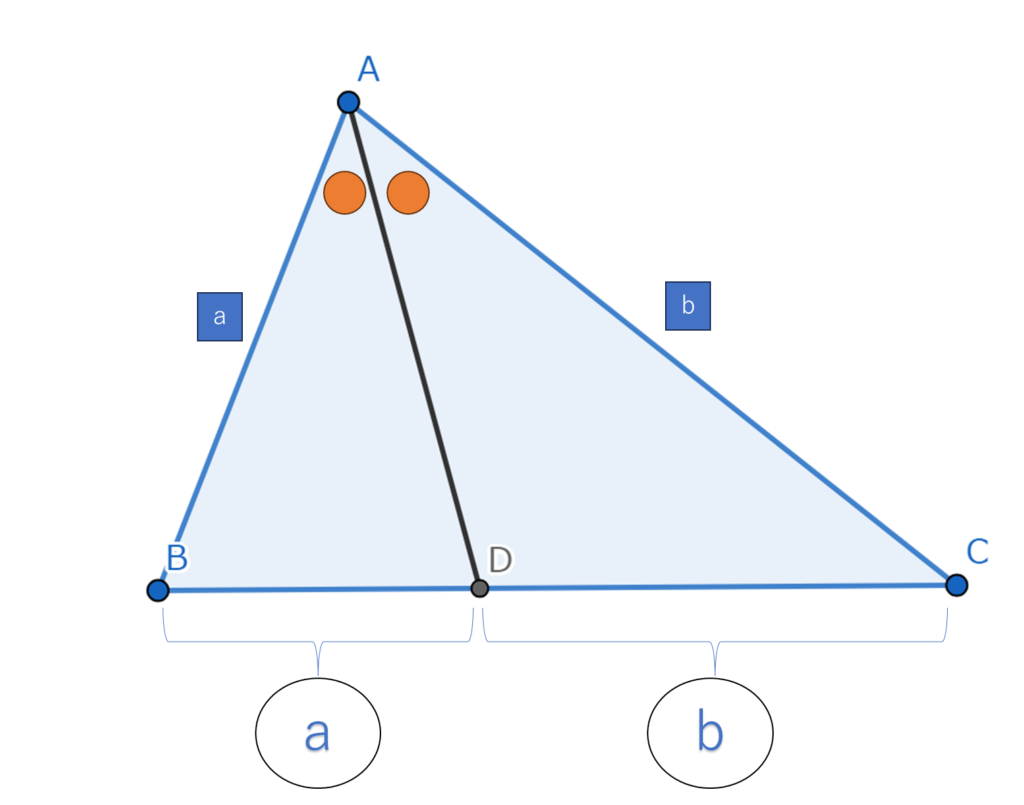
上の図で表すとBD:DC=a:bと表記できます。
ベクトルで表すと次のようにも表記できます。
\( \overrightarrow{AD} = \frac{b}{a+b}\overrightarrow{AB} + \frac{a}{a+b}\overrightarrow{AC} \)
さらに点Dは線分BC上にあるのでBD:DC=s:tとしてかつ、
s+t=1として考えることもできます。
\( \overrightarrow{AD} = (1-s)\overrightarrow{AB} + (s)\overrightarrow{AC} \)
外角の二等分線による外分
外角の二等分線についても、比の式が成立するので見ていきましょう。
△ABCについて∠Aの外角の二等分線を引き、
直線BCの交点を点Dとすると、図は次の通りになります。
ただし、説明用に線分ABの長さを9、線分ACの長さを4とします。
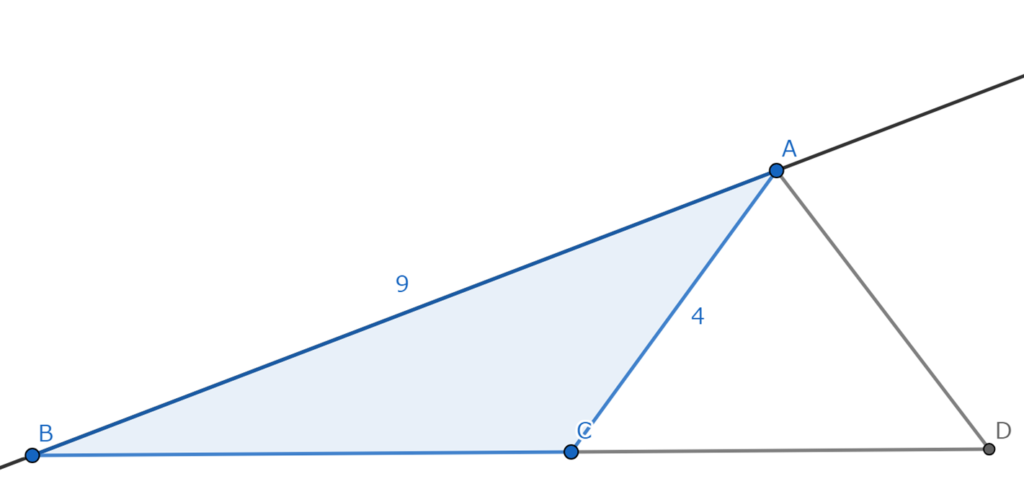
上の図に補助線を引きます。
線分ADに平行になる点Cを通る直線を引きます。
引いた直線と線分ABの交点を点Eとします。
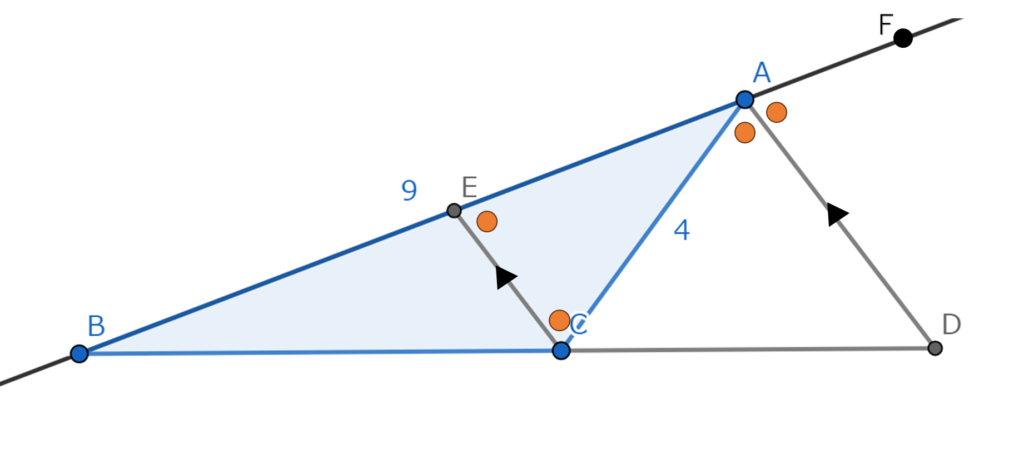
すると上の図のようになり以下のことが言えるようになります。
(説明用に直線ABのA側の先に点Fを置きます)
AD\(/\!/\)ECより、∠DAC=ACE、∠FAD=∠AEC …①
外角の二等分線より∠FAD=∠DAC…②
①②より∠AEC=∠ACEなので△AECはAE=AC=4の二等辺三角形といえる。
AD\(/\!/\)ECより、BA:AE=BD:CD=9:4
このことから三角形の外角の二等分線は、外角の向かい合う直線を
その内角をなす辺の長さの比で外分することができるといえます。
以上の例から三角形の外角の二等分線とその外角に向かい合う線分との交点は
次のような一般式で外分できます。
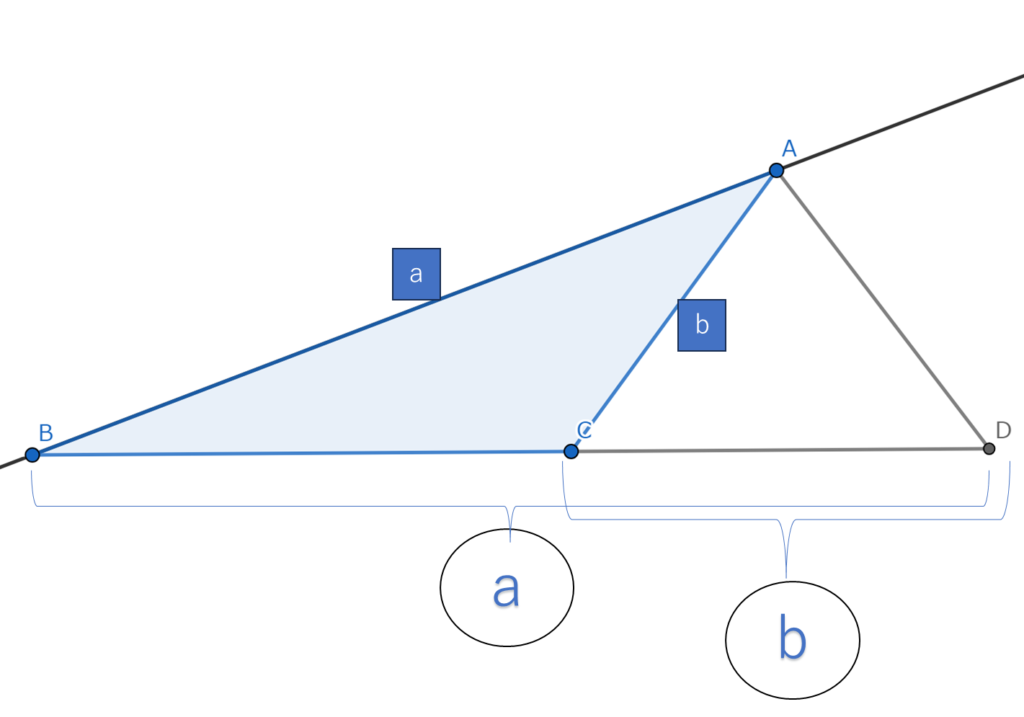
上の図で表すとBD:DC=a:bと表記できます。
ベクトルで表すと次のようにも表記できます。
\( \overrightarrow{AD} = \frac{-b}{a-b}\overrightarrow{AB} + \frac{a}{a-b}\overrightarrow{AC} \)
まとめ
二つ書いてきましたが、
内角の二等分線での内分、外角の二等分線での外分は
式の比がどちらもAB:AC=BD:CDになっていることが分かりました。
とはいえベクトル等で表記した時の式は
プラスマイナスの符号が変わっていることに注意しないといけませんが。
ということでほぼ忘れかけていた内分・外分のまとめの話でした。
今回はここまで。


コメント