カテナリーです。
数学検定準1級の数列の問題をやっていましたが、
解き方は分かっていても計算量の差が激しくて久々に困惑していました
(答え合っているのに数がきれいじゃなくて不安になっていた)
そこで特殊な数列を用いた問題と、解き方・計算量の部分も含めて
難易度表記してみました。全部で5問解説します。
和の形から数列を求める
難易度★★☆☆☆
例題1:次の第n項までの数列の和から一般項を求めなさい
\( S_n = 3n^2 + 5n \)
数列の和から一般項を求める問題です。
一般項は\( S_n – S_{n-1} \)とすることで第n項目の数となるので
単純に引き算をすれば求められます。
注意してきたいのは前述の引き算はn ≧ 2 の時にしか成立しないこと。
n≧2の計算が終わったらn=1でも成立するか確認しましょう。
部分分数分解で変形して和を求める
難易度★★★☆☆
例題2:次の和を求めなさい
\( \frac{1}{6 \cdot 8} + \frac{1}{8 \cdot 10} + \cdots + \frac{1}{(2n+4)(2n+6)} \)
例題のように分母が積の形の式になっている数列の和を考える場合は
これから紹介する部分分数分解が必要な場合があります。
一つの分数でまとめられているものを二つの分数で分けること、
分けるだけでなく分数同士で消せるように
形を直す必要があるので慣れるまでは難しいかもしれません。
一般式が分数で表されており、加えて部分分数分解で変形可能な数列です。
部分分数分解とは次のような変形を指します。
$$ \frac{1}{x(x+a)} = \frac{1}{a} \left\{ \frac{1}{x} – \frac{1}{x+a} \right\} $$
この部分分数分解を例題に当てはめると次のようになります。
$$ \frac{1}{(2n+4)(2n+6)} = \frac{1}{4} \left\{ \frac{1}{n+2} – \frac{1}{n+3} \right\} $$
変形した式で和を考えると次のようになります。
$$ \frac{1}{4} \left\{ \left( \frac{1}{3} – \frac{1}{4} \right) + \left( \frac{1}{4} – \frac{1}{5} \right) + \left( \frac{1}{5} – \frac{1}{6} \right) \cdots + \left( \frac{1}{n+2} – \frac{1}{n+3} \right) \right\} $$
このように丸括弧をまたいだ隣り合わせの分数同士で消すことができます。
問題によっては消すことができる分数が例題のような隣り合わせではなく
2つまたいだ先の分数同士が消える場合もあります。
階差数列から一般項を求める
難易度★★★☆☆
例題3:次の数列の一般項を求めなさい
3,5,9,15,23,33…
計算量を考えると階差数列次第にはなってきますが
そこまで多くはないのかなと思います。
問題によっては階差数列からさらに階差数列を考える
必要も出てくるのでそうなってくると計算が難しくなるかもしれません。
例題で出題している各数列の間を見るとその差は2,4,6,8,10…となっています。
これは初項2、公差2の等差数列となっていますね。
元の数列を\( a_n \)、差をとった数列を\( b_n \)としたとき
\( b_n = a_n – a_{n-1} ( n \geq 2 ) \) と表すことができるようになります。
このような数列を階差数列といいます。
階差数列は次のように表すことができます(ただしn≧2)
$$ a_n = a_1 + \displaystyle \sum_{i=1}^{n-1}b_i $$
この公式の\(a_{n}\),\(b_{n}\)にそれぞれ数列を当てはめて
計算すれば一般項を求めることができます。
求めたらn=1でも成立するか確認しましょう。
等差・等比数列が入り混じった数列から和を求める
難易度★★★★☆
例題4:次の一般項の第1項から第n項までの総和を求めなさい
\( 2n \cdot 3^{n-1} \)
等比数列と等差数列の混ざった数列は総和を求めるのが難しいです。
そのままシグマの式に当てめることができないので一工夫が必要です。
用意する例題の数字は比較的易しめですが
数字が大きくなったり約分しにくくなってくると計算ミスが
出やすくなるので難易度はやや高めなのかなの感じます。
S=この数列の第1項から第n項までの和
3S=Sに等比数列の公比である3をかけた和
これを次のように引いていくと
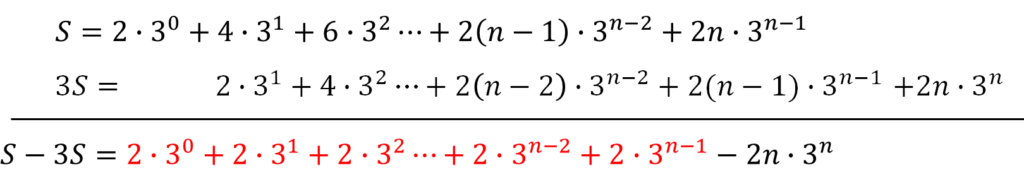
赤字で書かれている部分が等比数列の和になります。
これは公比分をかけて引き算をすることで等比数列の公差を
出すことができ、さらにそれをかっこでくくることにより
等比数列の形にすることができるようになったためです。
等差数列と等比数列が混ざっている場合はこのように
求める和に公比分をかけて引き算をしましょう。
群数列
難易度★★★★★
例題5:次の数列に関して以下の問いに答えなさい
\( 1,1,3,1,3,5,1,3,5,7 \cdots \)
(1)この数列の第20項はいくつか求めなさい
(2)第30項までの和はいくつか求めなさい
群数列とは数列を規則に従って区切って分けたものを指します。
数列を一定の規則で区切って考えた方が楽な場合があります。
区切った後は
「求めている項数は何群目の何番目なのか」もしくは
「第m群の第n番目は、第何項目に当たるのか」
という置き換えが非常に重要になってきます。
そのため計算量が普段よりも増えるため難易度は高い方だと思っています。
例題の数列を見てみると最初の1の次に1,3ときてまた1が続き3,5、
再び1がきて3,5,7とき来ているので、
1群進むごとに奇数が1個増えていると考えることができます。
よって例題の数列は次のように区切るとこのようになります。
\( 1, | 1,3, | 1,3,5, | 1,3,5,7 | \cdots \)
(1)についていくつかを考える前に
第20項目が何群目の何番目を考えてみましょう。
まずは何群目にあるのかを検討する必要があります。
規則性によって分けた群数列から
第1群には2個、第2群には2個、第3群には3個・・・と、
第m群にはm個数列が列挙されていることが分かります。
これは初項1、公差1の等差数列と考えることができます。
この数列の和は第m群の最後の数字が第何項かを表すことができます。
よって第m群の最後の数字は第\( \frac{1}{2}m(m+1) \)項目となります。
では、第20項目は第何群にあるでしょうか?次のようになります。
\( \frac{1}{2}(m-1)m < 20 ≦ \frac{1}{2}m(m+1)\)
これを満たす整数mは6だけなので第20項は第6群にあることになります。
続いて第6群の中の何番目かを考えましょう。
第5群の最後は\( \frac{1}{2}m(m+1) \) より第15項目なので
第6群の1番目は第16項目となります。
よって第20項目は第6群目の第5番目となります。
第6群目の数列は 1,3,5,7,9,11となるので5番目は9だということが分かります。
(2)についても第30項が何群目の何番目なのかを考えるところから始めます。
その後、各群の総和を順番に求めていけば答えることができます。
ここまで群数列の解き方について書いてきましたが
求めるために踏む段階が多いこともあり他の問題に比べて計算量が大変です。
なので自分は群数列は難易度が高いと感じました。
「分数の数列」や「第100項を求めなさい」とか複雑になってくると
さらに計算量が多くなるので慎重にこなしていきましょう。
以上、特殊な形の数列を用いた問題について5問触れてきました。
後半の問題は準1級の2次試験辺りにも出るらしいので合格のためには
しっかり押さえておきたいところですね。
今回の備忘録はこの辺で。
例題の答え
例題1:\( 6n+2 \)
例題2:\( \frac{n}{12(n+3)} \)
例題3:\( n(n+2) \)
例題4:\( 3^{n}n-\frac{1}{2}(3^n-1) \)
例題5(1):9
例題5(2):144



コメント